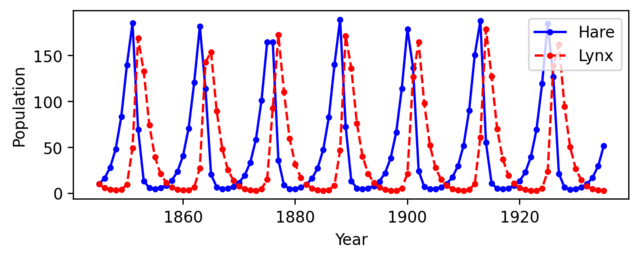
Figure 3.8: Discrete-time simulation of the predator–prey model

Chapter	System Modeling
Figure number	3.8
Figure title	Discrete-time simulation of the predator–prey model
GitHub URL	https://github.com/murrayrm/fbs2e-python/blob/main/figure-3.8-predator prey.py
Requires	python-control

Figure 3.8: Discrete-time simulation of the predator–prey model (3.13). Using the parameters $a=c=0.014$, $b_{h}(u)=0.6$, and $d_{l}=0.7$ in equation (3.13), the period and magnitude of the lynx and hare population cycles approximately match the data in Figure 3.7.

# figure-3.8-predator_prey.py - discrete-time simulation of predator–prey model # RMM, 15 May 20219 # # Figure 3.8: Discrete-time simulation of the predator–prey model # (3.13). Using the parameters a = c = 0.014, bh(u) = 0.6, and dl = # 0.7 in equation (3.13), the period and magnitude of the lynx and # hare population cycles approximately match the data in Figure 3.7. import control as ct import numpy as np import matplotlib.pyplot as plt # Define the dynamics of the predator prey system def predprey(t, x, u, params): # Parameter setup a = params.get('a', 0.014) / 365. bh0 = params.get('bh0', 0.6) / 365. c = params.get('c', 0.014) / 365. dl = params.get('dl', 0.7) / 365. # Map the states into local variable names H = x[0] L = x[1] # Compute the input bhu = bh0 + u # Compute the discrete updates dH = H + bhu * H - a * L * H dL = L + c * L * H - dl * L return [dH, dL] # Create a nonlinear I/O system (dt = days) io_predprey = ct.NonlinearIOSystem( predprey, None, inputs=('u'), outputs=('H', 'L'), states=('H', 'L'), name='predprey', dt=1/365) X0 = [10, 10] # Initial H, L T = np.linspace(1845, 1935, 90*365 + 1) # 90 years # Simulate the system response = ct.input_output_response(io_predprey, T, 0, X0) t, y = response.time, response.outputs # Downsample the responses to individual years yrs = t[::365] pop = y[:, ::365] # Plot the response plt.subplot(2, 1, 1) # Set the aspect ration to match the text plt.plot(yrs, pop[0], 'b-o', markersize=3) plt.plot(yrs, pop[1], 'r--o', markersize=3) plt.legend(["Hare", "Lynx"]) plt.xlabel("Year") plt.ylabel("Population")