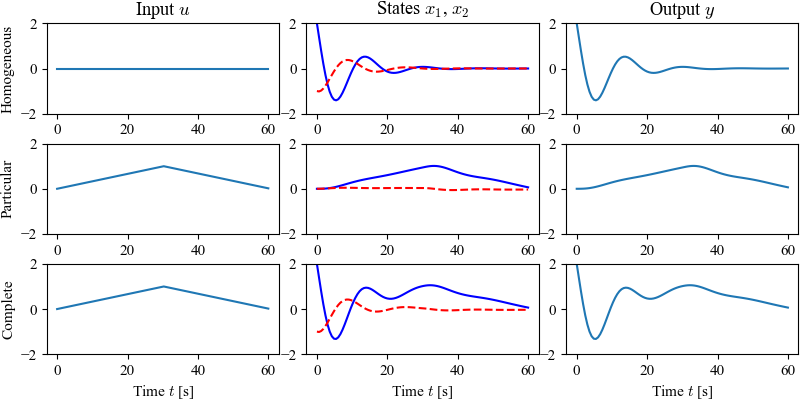
Figure 6.1: Superposition of homogeneous and particular solutions

Chapter	Linear Systems
Figure number	6.1
Figure title	Superposition of homogeneous and particular solutions
GitHub URL	https://github.com/murrayrm/fbs2e-python/blob/main/figure-6.1-superposition.py
Requires	python-control, springmass.py

Figure65.1: Superposition of homogeneous and particular solutions. The first row shows the input, state, and output corresponding to the initial condition response. The second row shows the same variables corresponding to zero initial condition but nonzero input. The third row is the complete solution, which is the sum of the two individual solutions.

<nowiki>

1. superposition.py - superposition of homogeneous and particular solutions
2. RMM, 19 Apr 2024

import matplotlib.pyplot as plt import numpy as np import control as ct import fbs # FBS plotting customizations

1. Spring mass system

from springmass import springmass # use spring mass dynamics sys = springmass / springmass(0) # normalize the response to 1 X0 = [2, -1] # initial condition

1. Create input vectors

tvec = np.linspace(0, 60, 100) u1 = 0 * tvec u2 = np.hstack([tvec[0:50]/tvec[50], 1 - tvec[0:50]/tvec[50]])

1. Run simulations for the different cases

homogeneous = ct.forced_response(sys, tvec, u1, X0=X0) particular = ct.forced_response(sys, tvec, u2) complete = ct.forced_response(sys, tvec, u1 + u2, X0=X0)

1. Plot results

fig, axs = plt.subplots(3, 3, figsize=[8, 4], layout='tight') for i, resp in enumerate([homogeneous, particular, complete]):

   axs[i, 0].plot(resp.time, resp.inputs)
   axs[0, 0].set_title("Input $u$")
   axs[i, 0].set_ylim(-2, 2)
   
   axs[i, 1].plot(
       resp.time, resp.states[0], 'b',
       resp.time, resp.states[1], 'r--')
   axs[0, 1].set_title("States $x_1$, $x_2$")
   axs[i, 1].set_ylim(-2, 2)

   axs[i, 2].plot(resp.time, resp.outputs)
   axs[0, 2].set_title("Output $y$")
   axs[i, 2].set_ylim(-2, 2)

1. Label the plots

axs[0, 0].set_ylabel("Homogeneous") axs[1, 0].set_ylabel("Particular") axs[2, 0].set_ylabel("Complete") for i in range(3):

   axs[2, i].set_xlabel("Time $t$ [s]")

1. Save the figure

fbs.savefig('figure-6.1-superposition.png') <nowiki>