Difference between revisions of "Figure 5.16: Dynamics of a genetic switch"
Jump to navigation
Jump to search
(Created page with "{{Figure |Chapter=Dynamic Behavior |Figure number=5.16 |Sort key=516 |Figure title=Dynamics of a genetic switch |GitHub URL=https://github.com/murrayrm/fbs2e-python/blob/main/...") |
m |
||
| (One intermediate revision by the same user not shown) | |||
| Line 8: | Line 8: | ||
[[Image:figure-5.16-genswitch_dynamics.png]] | [[Image:figure-5.16-genswitch_dynamics.png]] | ||
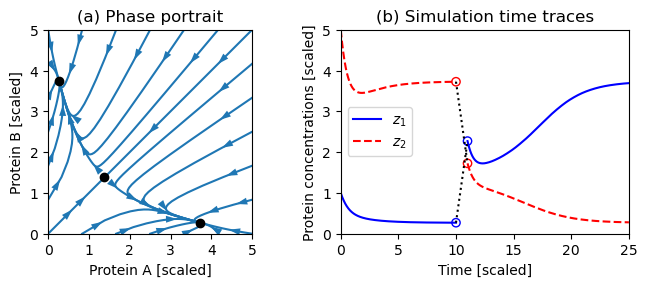
| − | Figure 5.16: Dynamics of a genetic switch. The phase portrait on the left shows that the switch has three equilibrium points, corresponding to protein A having a concentration greater than, equal to, or less than protein B. The equilibrium point with equal protein concentrations is unstable, but the other equilibrium points are stable. The simulation on the right shows the time response of the system starting from two different initial conditions. The initial portion of the curve corresponds to initial concentrations <math>z(0) = (1, 5)</math> and converges to the equilibrium point where <math>z_{1e} < z_{2e}</math>. At time <math>t = 10</math>, the concentrations are perturbed by +2 in <math>z_1</math> and −2 in <math>z_2</math>, moving the state into the region of the state space whose solutions converge to the equilibrium point where <math>z_{2e} < z_{1e}</math>. | + | '''Figure 5.16''': Dynamics of a genetic switch. The phase portrait on the left shows that the switch has three equilibrium points, corresponding to protein A having a concentration greater than, equal to, or less than protein B. The equilibrium point with equal protein concentrations is unstable, but the other equilibrium points are stable. The simulation on the right shows the time response of the system starting from two different initial conditions. The initial portion of the curve corresponds to initial concentrations <math>z(0) = (1, 5)</math> and converges to the equilibrium point where <math>z_{1e} < z_{2e}</math>. At time <math>t = 10</math>, the concentrations are perturbed by +2 in <math>z_1</math> and −2 in <math>z_2</math>, moving the state into the region of the state space whose solutions converge to the equilibrium point where <math>z_{2e} < z_{1e}</math>. |
<nowiki> | <nowiki> | ||
# example-5.13-genetic_switch.py - Genetic switch dynamics | # example-5.13-genetic_switch.py - Genetic switch dynamics | ||
# RMM, 17 Nov 2024 | # RMM, 17 Nov 2024 | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
# | # | ||
# Figure 5.16: Dynamics of a genetic switch. The phase portrait on the left | # Figure 5.16: Dynamics of a genetic switch. The phase portrait on the left | ||
| Line 32: | Line 26: | ||
# the state space whose solutions converge to the equilibrium point where | # the state space whose solutions converge to the equilibrium point where | ||
# z2e < z1e. | # z2e < z1e. | ||
| − | |||
import control as ct | import control as ct | ||
Latest revision as of 02:14, 18 November 2024
| Chapter | Dynamic Behavior |
|---|---|
| Figure number | 5.16 |
| Figure title | Dynamics of a genetic switch |
| GitHub URL | https://github.com/murrayrm/fbs2e-python/blob/main/example-5.13-genetic switch.py |
| Requires | python-control |
Figure 5.16: Dynamics of a genetic switch. The phase portrait on the left shows that the switch has three equilibrium points, corresponding to protein A having a concentration greater than, equal to, or less than protein B. The equilibrium point with equal protein concentrations is unstable, but the other equilibrium points are stable. The simulation on the right shows the time response of the system starting from two different initial conditions. The initial portion of the curve corresponds to initial concentrations and converges to the equilibrium point where . At time , the concentrations are perturbed by +2 in and −2 in , moving the state into the region of the state space whose solutions converge to the equilibrium point where .
# example-5.13-genetic_switch.py - Genetic switch dynamics
# RMM, 17 Nov 2024
#
# Figure 5.16: Dynamics of a genetic switch. The phase portrait on the left
# shows that the switch has three equilibrium points, corresponding to
# protein A having a concentration greater than, equal to, or less than
# protein B. The equilibrium point with equal protein concentrations is
# unstable, but the other equilibrium points are stable. The simulation on
# the right shows the time response of the system starting from two
# different initial conditions. The initial portion of the curve
# corresponds to initial concentrations z(0) = (1, 5) and converges to the
# equilibrium point where z1e < z2e. At time t = 10, the concentrations are
# perturbed by +2 in z1 and −2 in z2, moving the state into the region of
# the state space whose solutions converge to the equilibrium point where
# z2e < z1e.
import control as ct
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp
from scipy.optimize import fsolve
ct.use_fbs_defaults()
#
# System dynamics
#
# Switch parameters
genswitch_params = {'mu': 4, 'n': 2}
def genswitch_dynamics(t, x, u, params):
mu = params.get('mu')
n = params.get('n')
z1, z2 = x
dz1 = mu / (1 + z2**n) - z1
dz2 = mu / (1 + z1**n) - z2
return [dz1, dz2]
genswitch_model = ct.nlsys(
genswitch_dynamics, None, states=2, inputs=None, params=genswitch_params)
#
# 5.16 (a) Phase portrait
#
fig = plt.figure(constrained_layout=True)
gs = fig.add_gridspec(2, 2)
ax = fig.add_subplot(gs[0, 0]) # first row, first column
ct.phase_plane_plot(
genswitch_model, [0, 5, 0, 5], 10, gridspec=[7, 7], ax=ax,
plot_separatrices=False)
ax.axis('scaled')
ax.axis([0, 5, 0, 5])
ax.set_xticks([0, 1, 2, 3, 4, 5]) # defaults are different than y axis (?)
ax.set_xlabel("Protein A [scaled]")
ax.set_ylabel("Protein B [scaled]")
ax.set_title('(a) Phase portrait')
#
# 5.16 (b) Time traces
#
ax = fig.add_subplot(gs[0, 1]) # first row, second column
# Solve the ODE for the first segment
sol1 = ct.input_output_response(
genswitch_model, np.linspace(0, 10, 1000), 0, [1, 5])
# Solve the ODE for the second segment
sol2 = ct.input_output_response(
genswitch_model, np.linspace(11, 25, 1000), 0,
[sol1.states[0, -1] + 2, sol1.states[1, -1] - 2])
# Second plot: Time traces
ax.plot(sol1.time, sol1.outputs[0], 'b-', label='$z_1$')
ax.plot(sol1.time, sol1.outputs[1], 'r--', label='$z_2$')
ax.plot(sol2.time, sol2.outputs[0], 'b-')
ax.plot(sol2.time, sol2.outputs[1], 'r--')
ax.plot(
[sol1.time[-1], sol2.time[0]], [sol1.outputs[0, -1], sol2.outputs[0, -0]],
'k:')
ax.plot(
[sol1.time[-1], sol2.time[0]], [sol1.outputs[1, -1], sol2.outputs[1, -0]],
'k:')
ax.scatter(
[sol1.time[-1], sol2.time[0]], [sol1.outputs[0, -1], sol2.outputs[0, 0]],
edgecolors='b', facecolors='none', marker='o')
ax.scatter(
[sol1.time[-1], sol2.time[0]], [sol1.outputs[1, -1], sol2.outputs[1, 0]],
edgecolors='r', facecolors='none', marker='o')
ax.axis([0, 25, 0, 5])
ax.set_xlabel('Time [scaled]')
ax.set_ylabel('Protein concentrations [scaled]')
ax.legend()
ax.set_title('(b) Simulation time traces')
# Save the second figure
plt.savefig("figure-5.16-genswitch_dynamics.png", bbox_inches='tight')