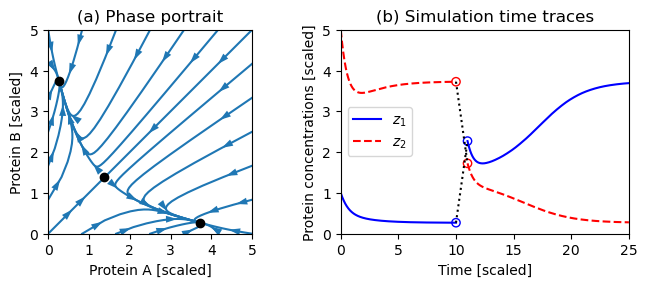
Figure 5.16: Dynamics of a genetic switch

Chapter	Dynamic Behavior
Figure number	5.16
Figure title	Dynamics of a genetic switch
GitHub URL	https://github.com/murrayrm/fbs2e-python/blob/main/example-5.13-genetic switch.py
Requires	python-control

Figure 5.16: Dynamics of a genetic switch. The phase portrait on the left shows that the switch has three equilibrium points, corresponding to protein A having a concentration greater than, equal to, or less than protein B. The equilibrium point with equal protein concentrations is unstable, but the other equilibrium points are stable. The simulation on the right shows the time response of the system starting from two different initial conditions. The initial portion of the curve corresponds to initial concentrations $z(0)=(1,5)$ and converges to the equilibrium point where $z_{1e}<z_{2e}$. At time $t=10$, the concentrations are perturbed by +2 in $z_{1}$ and −2 in $z_{2}$, moving the state into the region of the state space whose solutions converge to the equilibrium point where $z_{2e}<z_{1e}$.

# example-5.13-genetic_switch.py - Genetic switch dynamics
# RMM, 17 Nov 2024
#
# Figure 5.16: Dynamics of a genetic switch. The phase portrait on the left
# shows that the switch has three equilibrium points, corresponding to
# protein A having a concentration greater than, equal to, or less than
# protein B. The equilibrium point with equal protein concentrations is
# unstable, but the other equilibrium points are stable. The simulation on
# the right shows the time response of the system starting from two
# different initial conditions. The initial portion of the curve
# corresponds to initial concentrations z(0) = (1, 5) and converges to the
# equilibrium point where z1e < z2e. At time t = 10, the concentrations are
# perturbed by +2 in z1 and −2 in z2, moving the state into the region of
# the state space whose solutions converge to the equilibrium point where
# z2e < z1e.

import control as ct
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp
from scipy.optimize import fsolve
ct.use_fbs_defaults()

#
# System dynamics
#

# Switch parameters
genswitch_params = {'mu': 4, 'n': 2}

def genswitch_dynamics(t, x, u, params):
    mu = params.get('mu')
    n = params.get('n')
    z1, z2 = x
    dz1 = mu / (1 + z2**n) - z1
    dz2 = mu / (1 + z1**n) - z2
    return [dz1, dz2]

genswitch_model = ct.nlsys(
    genswitch_dynamics, None, states=2, inputs=None, params=genswitch_params)

#
# 5.16 (a) Phase portrait
#

fig = plt.figure(constrained_layout=True)
gs = fig.add_gridspec(2, 2)
ax = fig.add_subplot(gs[0, 0])  # first row, first column

ct.phase_plane_plot(
    genswitch_model, [0, 5, 0, 5], 10, gridspec=[7, 7], ax=ax,
    plot_separatrices=False)

ax.axis('scaled')
ax.axis([0, 5, 0, 5])
ax.set_xticks([0, 1, 2, 3, 4, 5])       # defaults are different than y axis (?)
ax.set_xlabel("Protein A [scaled]")
ax.set_ylabel("Protein B [scaled]")
ax.set_title('(a) Phase portrait')

#
# 5.16 (b) Time traces
#

ax = fig.add_subplot(gs[0, 1])  # first row, second column

# Solve the ODE for the first segment
sol1 = ct.input_output_response(
    genswitch_model, np.linspace(0, 10, 1000), 0, [1, 5])

# Solve the ODE for the second segment
sol2 = ct.input_output_response(
    genswitch_model, np.linspace(11, 25, 1000), 0,
    [sol1.states[0, -1] + 2, sol1.states[1, -1] - 2])

# Second plot: Time traces
ax.plot(sol1.time, sol1.outputs[0], 'b-', label='$z_1$')
ax.plot(sol1.time, sol1.outputs[1], 'r--', label='$z_2$')
ax.plot(sol2.time, sol2.outputs[0], 'b-')
ax.plot(sol2.time, sol2.outputs[1], 'r--')
ax.plot(
    [sol1.time[-1], sol2.time[0]], [sol1.outputs[0, -1], sol2.outputs[0, -0]],
    'k:')
ax.plot(
    [sol1.time[-1], sol2.time[0]], [sol1.outputs[1, -1], sol2.outputs[1, -0]],
    'k:')
ax.scatter(
    [sol1.time[-1], sol2.time[0]], [sol1.outputs[0, -1], sol2.outputs[0, 0]],
    edgecolors='b', facecolors='none', marker='o')
ax.scatter(
    [sol1.time[-1], sol2.time[0]], [sol1.outputs[1, -1], sol2.outputs[1, 0]],
    edgecolors='r', facecolors='none', marker='o')
ax.axis([0, 25, 0, 5])
ax.set_xlabel('Time [scaled]')
ax.set_ylabel('Protein concentrations [scaled]')
ax.legend()
ax.set_title('(b) Simulation time traces')

# Save the second figure
plt.savefig("figure-5.16-genswitch_dynamics.png", bbox_inches='tight')