Figure 3.2: Illustration of a state model
Jump to navigation
Jump to search
| Chapter | System Modeling |
|---|---|
| Figure number | 3.2 |
| Figure title | Illustration of a state model |
| GitHub URL | https://github.com/murrayrm/fbs2e-python/blob/main/figure-3.2-state model.py |
| Requires | python-control |
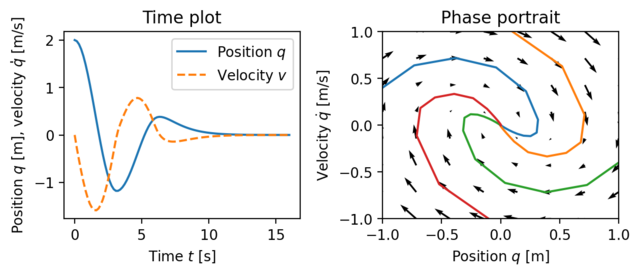
Figure 3.2: Illustration of a state model. A state model gives the rate of change of the state as a function of the state. The plot on the left shows the evolution of the state as a function of time. The plot on the right, called a phase portrait, shows the evolution of the states relative to each other, with the velocity of the state denoted by arrows.
# figure-3.2-state_mode.py - illustration of a state model
# RMM, 2 Jul 2021
#
# Figure 3.2: Illustration of a state model. A state model gives the rate of
# change of the state as a function of the state. The plot on the left shows
# the evolution of the state as a function of time. The plot on the right,
# called a phase portrait, shows the evolution of the states relative to
# each other, with the velocity of the state denoted by arrows.
#
import numpy as np
import scipy as sp
import matplotlib.pyplot as plt
import control as ct
#
# Spring mass system with nonlinear dampling
#
# This function gives the dynamics for a dampled oscillator with nonlinear
# damping. The states of the system are
#
# x[0] position
# x[1] velocity
#
# The nonlinear damping is implemented as a change in the linear damping
# coefficient at a small velocity. This is intended to roughly correspond
# to some sort of stiction (and give an interesting phase portrait). The
# default parameters for the system are given by
#
# m = 1 mass, kg
# k = 1 spring constant, N/m
# b1 = 1 damping constant near origin, N-sec/m
# b2 = 0.01 damping constant away from origin, N-sec/m
# dth = 0.5 threshold for switching between damping
#
# This corresponds to a fairly lightly damped oscillator away from the origin.
def nlspringmass(x, t, u=0, m=1, k=1, b1=2, b2=0.01, dth=0.2):
# Compute the friction force
if abs(x[1]) < dth:
Fb = b1 * x[1];
elif x[1] < 0:
Fb = -b1 * dth \
+ b2 * (x[1] + dth);
else:
Fb = b1 * dth \
+ b2 * (x[1] - dth);
# Return the time derivative of the state
return np.array([x[1], -k/m * x[0] - Fb/m])
#
# (a) Simulation of the nonlinear spring mass system
#
plt.subplot(2, 2, 1)
t = np.linspace(0, 16, 100)
y = sp.integrate.odeint(nlspringmass, [2, 0], t)
plt.plot(t, y[:, 0], '-', t, y[:, 1], '--')
plt.xlabel('Time $t$ [s]')
plt.ylabel('Position $q$ [m], velocity $\dot q$̇ [m/s]')
plt.title('Time plot')
plt.legend(['Position $q$', 'Velocity $v$'])
#
# (b) Generate a phase plot for the damped oscillator
#
plt.subplot(2, 2, 2)
ct.phase_plot(
nlspringmass, # dynamics
(-1, 1, 8), (-1, 1, 8), # X, Y range, npoints
scale=0.2,
X0=[[-1, 0.4], [0.1, 1], [1, -0.4], [-0.1, -1]])
plt.xlabel('Position $q$ [m]')
plt.ylabel('Velocity $\dot q$ [m/s]')
plt.title('Phase portrait')
plt.axis([-1, 1, -1, 1])
plt.tight_layout()