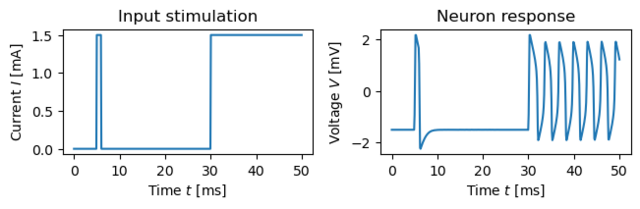
Figure 3.28: Response of a neuron to a current input
Jump to navigation
Jump to search
| Chapter | System Modeling |
|---|---|
| Figure number | 28 |
| Figure title | Response of a neuron to a current input |
| GitHub URL | https://github.com/murrayrm/fbs2e-python/blob/main/example-3.19-fitzhugh nagumo.py |
| Requires | python-control |
Figure 3.28: Response of a neuron to a current input. The current input is shown in (a) and the neuron voltage V in (b). The simulation was done using the FitzHugh–Nagumo model (Exercise 3.11).
# example-3.19-fitzhugh_nagumo.py - nerve cell dynamics
# RMM, 30 Aug 2021
#
# Figure 3.28: Response of a neuron to a current input. The current
# input is shown in (a) and the neuron voltage V in (b). The
# simulation was done using the FitzHugh–Nagumo model (Exercise 3.11).
import control as ct
import numpy as np
import matplotlib.pyplot as plt
ct.use_fbs_defaults()
#
# System dynamics
#
# FitzHugh-Nagumo dynamics (from KJA)
def fitzhugh_nagumo_dynamics(t, x, u, params):
dx = np.zeros(3)
# Get the system state
V = x[0]
R = x[1]
# Compute the dim derivative
dx[0] = 10 * (V - (V**3) / 3 - R + u)
dx[1] = 0.8 * (-R + 1.25 * V + 1.5)
dx[2] = 1
return dx
# Set up an input/output system
sys = ct.NonlinearIOSystem(
updfcn=fitzhugh_nagumo_dynamics, states=3, inputs=1, outputs=3)
# Set up the plotting grid to match the layout in the book
fig = plt.figure(constrained_layout=True)
gs = fig.add_gridspec(3, 2)
#
# (a) Current input
#
fig.add_subplot(gs[0, 0]) # first row, first column
# Set up input stimulation
t = np.linspace(0, 50, 500)
u = np.zeros_like(t)
u[t >= 5] = 1.5 # start of short input pulse
u[t >= 6] = 0 # end of short input pulse
u[t >= 30] = 1.5 # longer input pulse
# Initial state
x0 = [-1.5, -3/8, 0]
response = ct.input_output_response(sys, t, u, x0)
plt.plot(response.time, response.inputs[0])
plt.xlabel("Time $t$ [ms]")
plt.ylabel("Current $I$ [mA]")
plt.title("Input stimulation")
#
# (b) Neuron response
#
fig.add_subplot(gs[0, 1]) # first row, second column
plt.plot(response.time, response.states[0])
plt.xlabel("Time $t$ [ms]")
plt.ylabel("Voltage $V$ [mV]")
plt.title("Neuron response")
# Save the figure
plt.savefig("figure-3.19-fitzhugh_nagumo.png", bbox_inches='tight')