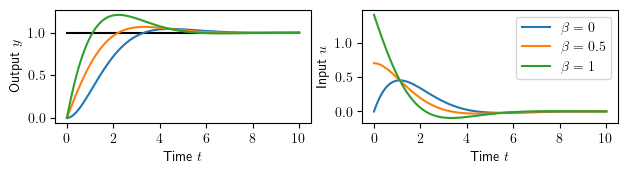
Figure 2.11: Response to a step change in the reference signal for a system with a PI controller having two degrees of freedom
Jump to navigation
Jump to search
| Chapter | Feedback Principles |
|---|---|
| Figure number | 11 |
| Figure title | Response to a step change in the reference signal for a system with a PI controller having two degrees of freedom |
| GitHub URL | https://github.com/murrayrm/fbs2e-python/blob/main/figure-2.11-2dof stepresp.py |
| Requires | python-control |
Figure 2.11: Response to a step change in the reference signal for a system with a PI controller having two degrees of freedom. The process transfer function is and the controller gains are , , and , , and .
# figure-2.8-PI_step_reesponses.py - step responses for P/PI controllers
# RMM, 21 Jun 2021
#
# Step responses for a first-order, closed loop system with proportional
# control and PI control. The process transfer function is P = 2/(s + 1).
# The controller gains for proportional control are k_p = 0, 0.5, 1, and
# 2. The PI controller is designed using equation (2.28) with zeta_c = 0.707
# and omega_c = 0.707, 1, and 2, which gives the controller parameters k_p =
# 0, 0.207, and 0.914 and k_i = 0.25, 0.50, and 2.
#
import numpy as np
import matplotlib.pyplot as plt
import control as ct
# Process model
b = 2; a = 1
P = ct.tf([b], [1, a])
# Set the simulation time vector
time = np.linspace(0, 8, 100)
#
# Proportional control
#
# Choose gains to use
kp_gains = [0, 0.5, 1, 2]
for kp in kp_gains:
Gyv = ct.tf([b], [1, a + b*kp])
Guv = ct.tf([-b*kp], [1, a + b*kp], dt=0) # force kp=0 to be cts time
t, y = ct.step_response(Gyv, time)
t, u = ct.step_response(Guv, time)
if 'p_y_ax' not in locals():
p_y_ax = plt.subplot(3, 2, 1)
plt.ylabel('Output $y$')
plt.title('Proportional control')
p_y_ax.plot(t, y)
if 'p_u_ax' not in locals():
p_u_ax = plt.subplot(3, 2, 3)
plt.ylabel('Input $u$')
plt.xlabel('Normalized time $at$')
p_u_ax.plot(t, u, label="kp = %0.3g" % kp)
# Label proportional control curves
p_u_ax.legend()
#
# PI control
#
# Figure out frequency of critical damping
zeta = 0.707
wc = a / 2 / zeta
# Plot results for different resonate frequencies
wc_list = [wc, 1, 2]
for wc in wc_list:
kp = (2 * zeta * wc - a) / b
ki = wc**2 / b
Gyv = ct.tf([b, 0], [1, a + b*kp, b*ki])
Guv = -ct.tf([b*kp, b*ki], [1, a + b*kp, b*ki], dt=0)
t, y = ct.step_response(Gyv, time)
t, u = ct.step_response(Guv, time)
if 'pi_y_ax' not in locals():
pi_y_ax = plt.subplot(3, 2, 2)
plt.ylabel('Output $y$')
plt.title('Proportional-integral control')
pi_y_ax.plot(t, y)
if 'pi_u_ax' not in locals():
pi_u_ax = plt.subplot(3, 2, 4)
plt.ylabel('Input $u$')
plt.xlabel('Normalized time $at$')
pi_u_ax.plot(t, u, label="wc = %0.3g" % wc)
# Label PI curves
pi_u_ax.legend()
# Overalll figure labeling
plt.tight_layout()