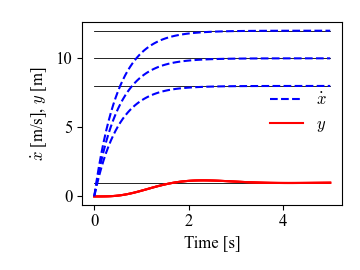
Figure 8.13: Vehicle steering using gain scheduling

Chapter	Output Feedback
Figure number	8.13
Figure title	Vehicle steering using gain scheduling
GitHub URL
Requires	python-control

Figure 8.13: Vehicle steering using gain scheduling. (a) Vehicle configuration consists of the x, y position of the vehicle, its angle with respect to the road, and the steering wheel angle. (b) Step responses for the vehicle lateral position (solid) and forward velocity (dashed). Gain scheduling is used to set the feedback controller gains for the different forward velocities.

<nowiki>

1. steering-gainsched.py - gain scheduled control for vehicle steering
2. RMM, 8 May 2019 (updated 6 Oct 2021)

import numpy as np import control as ct from cmath import sqrt import matplotlib.pyplot as mpl

2. Vehicle steering dynamics
4. The vehicle dynamics are given by a simple bicycle model. We take the state
5. of the system as (x, y, theta) where (x, y) is the position of the vehicle
6. in the plane and theta is the angle of the vehicle with respect to
7. horizontal. The vehicle input is given by (v, phi) where v is the forward
8. velocity of the vehicle and phi is the angle of the steering wheel. The
9. model includes saturation of the vehicle steering angle.
11. System state: x, y, theta
12. System input: v, phi
13. System output: x, y
14. System parameters: wheelbase, maxsteer

def vehicle_update(t, x, u, params):

   # Get the parameters for the model
   l = params.get('wheelbase', 3.)         # vehicle wheelbase
   phimax = params.get('maxsteer', 0.5)    # max steering angle (rad)

   # Saturate the steering input
   phi = np.clip(u[1], -phimax, phimax)

   # Return the derivative of the state
   return np.array([
       np.cos(x[2]) * u[0],            # xdot = cos(theta) v
       np.sin(x[2]) * u[0],            # ydot = sin(theta) v
       (u[0] / l) * np.tan(phi)        # thdot = v/l tan(phi)
   ])

def vehicle_output(t, x, u, params):

   return x                            # return x, y, theta (full state)

1. Define the vehicle steering dynamics as an input/output system

vehicle = ct.NonlinearIOSystem(

   vehicle_update, vehicle_output, states=3, name='vehicle',
   inputs=('v', 'phi'),
   outputs=('x', 'y', 'theta'))

2. Gain scheduled controller
4. For this system we use a simple schedule on the forward vehicle velocity and
5. place the poles of the system at fixed values. The controller takes the
6. current and desired vehicle position and orientation plus the velocity
7. velocity as inputs, and returns the velocity and steering commands.
9. System state: none
10. System input: x, y, theta, xd, yd, thetad, vd, phid
11. System output: v, phi
12. System parameters: longpole, latomega_c, latzeta_c

def control_output(t, x, u, params):

   # Get the controller parameters
   longpole = params.get('longpole', -2.)
   latomega_c = params.get('latomega_c', 2)
   latzeta_c = params.get('latzeta_c', 0.5)
   l = params.get('wheelbase', 3)
   
   # Extract the system inputs and compute the errors
   x, y, theta, xd, yd, thetad, vd, phid = u
   ex, ey, etheta = x - xd, y - yd, theta - thetad

   # Determine the controller gains
   lambda1 = -longpole
   a1 = 2 * latzeta_c * latomega_c
   a2 = latomega_c**2

   # Compute and return the control law
   v = vd - lambda1 * ex
   if vd != 0:
       phi = phid - ((a2 * l) / vd**2) * ey - ((a1 * l) / vd) * etheta
   else:
       # We aren't moving, so don't turn the steering wheel
       phi = phid
   
   return  np.array([v, phi])

1. Define the controller as an input/output system

controller = ct.NonlinearIOSystem(

   None, control_output, name='controller',            # static system
   inputs=('x', 'y', 'theta', 'xd', 'yd', 'thetad',    # system inputs
           'vd', 'phid'),
   outputs=('v', 'phi')                                # system outputs

)

2. Reference trajectory subsystem
4. The reference trajectory block generates a simple trajectory for the system
5. given the desired speed (vref) and lateral position (yref). The trajectory
6. consists of a straight line of the form (vref * t, yref, 0) with nominal
7. input (vref, 0).
9. System state: none
10. System input: vref, yref
11. System output: xd, yd, thetad, vd, phid
12. System parameters: none

def trajgen_output(t, x, u, params):

   vref, yref = u
   return np.array([vref * t, yref, 0, vref, 0])

1. Define the trajectory generator as an input/output system

trajgen = ct.NonlinearIOSystem(

   None, trajgen_output, name='trajgen',
   inputs=('vref', 'yref'),
   outputs=('xd', 'yd', 'thetad', 'vd', 'phid'))

2. System construction
4. The input to the full closed loop system is the desired lateral position and
5. the desired forward velocity. The output for the system is taken as the
6. full vehicle state plus the velocity of the vehicle.
8. We construct the system using the InterconnectedSystem constructor and using
9. signal labels to keep track of everything.

steering = ct.interconnect(

   # List of subsystems
   (trajgen, controller, vehicle), name='steering',

   # System inputs
   inplist=['trajgen.vref', 'trajgen.yref'],
   inputs=['yref', 'vref'],

   #  System outputs
   outlist=['vehicle.x', 'vehicle.y', 'vehicle.theta', 'controller.v',
            'controller.phi'],
   outputs=['x', 'y', 'theta', 'v', 'phi']

)

1. Set up the simulation conditions

yref = 1 T = np.linspace(0, 5, 100)

1. Set up a figure for plotting the results

mpl.figure(figsize=[3.2, 2.4], tight_layout=True)

1. Plot the reference trajectory for the y position

mpl.plot([0, 5], [yref, yref], 'k--')

1. Find the signals we want to plot

y_index = steering.find_output('y') v_index = steering.find_output('v')

1. Do an iteration through different speeds

for vref in [8, 10, 12]:

   # Simulate the closed loop controller response
   tout, yout = ct.input_output_response(
       steering, T, [vref * np.ones(len(T)), yref * np.ones(len(T))])

   # Plot the reference speed
   mpl.plot([0, 5], [vref, vref], 'k--')

   # Plot the system output
   y_line, = mpl.plot(tout, yout[y_index, :], 'r')  # lateral position
   v_line, = mpl.plot(tout, yout[v_index, :], 'b')  # vehicle velocity

1. Add axis labels

mpl.xlabel('Time [s]') mpl.ylabel('$x$ vel [m/s], $y$ pos [m]') mpl.legend((v_line, y_line), ('$v$', '$y$'), loc='center right', frameon=False)

1. Save the figure

mpl.savefig('steering-gainsched.pdf') <wiki>