Figure 3.22: Queuing dynamics

Chapter	System Modeling
Figure number	22
Figure title	Queuing dynamics
GitHub URL	https://github.com/murrayrm/fbs2e-python/blob/main/example-3.15-queuing systems.py
Requires	python-control

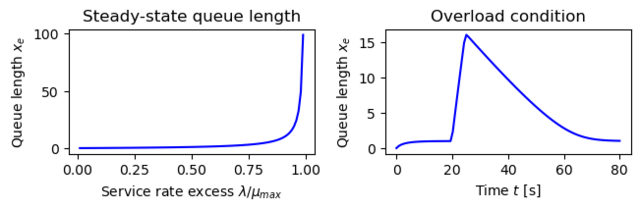
Figure 3.22: Queuing dynamics. (a) The steady-state queue length as a function of $\lambda /\mu _{\text{max}}$. (b) The behavior of the queue length when there is a temporary overload in the system. The solid line shows a realization of an event-based simulation, and the dashed line shows the behavior of the flow model (3.33). The maximum service rate is $\mu _{max}=1$, and the arrival rate starts at $\lambda =0.5$. The arrival rate is increased to $\lambda =4$ at time 20, and it returns to $\lambda =0.5$ at # time 25.

# example-3.15-queuing_systems.py - Queuing system modeling
# RMM, 29 Aug 2021
#
# Figure 3.22: Queuing dynamics. (a) The steady-state queue length as a
# function of $\lambda/\mu_{max}$. (b) The behavior of the queue length when
# there is a temporary overload in the system. The solid line shows a
# realization of an event-based simulation, and the dashed line shows the
# behavior of the flow model (3.33). The maximum service rate is $\mu_{max}
# = 1$, and the arrival rate starts at $\lambda = 0.5$. The arrival rate is
# increased to $\lambda = 4$ at time 20, and it returns to $\lambda =0.5$ at
# time 25.
#

import control as ct
import numpy as np
import matplotlib.pyplot as plt

# Queing parameters 

# Queuing system model (KJA, 2006)
def queuing_model(t, x, u, params={}):
    # Define default parameters
    mu = params.get('mu', 1)

    # Get the current load
    lambda_ = u

    # Return the change in queue size
    return np.array(lambda_ - mu * x[0] / (1 + x[0]))

# Create I/O system representation
queuing_sys = ct.NonlinearIOSystem(
    updfcn=queuing_model, inputs=1, outputs=1, states=1)

# Set up the plotting grid to match the layout in the book
fig = plt.figure(constrained_layout=True)
gs = fig.add_gridspec(3, 2)

#
# (a) The steady-state queue length as a function of $\lambda/\mu_{max}$.
#

fig.add_subplot(gs[0, 0])       # first row, first column

# Steady state queue length
x = np.linspace(0.01, 0.99, 100)
plt.plot(x, x / (1 - x), 'b-')

# Label the plot
plt.xlabel(r"Service rate excess $\lambda/\mu_{max}$")
plt.ylabel(r"Queue length $x_{e}$")
plt.title("Steady-state queue length")

#
# (b) The behavior of the queue length when there is a temporary overload
# in the system. The solid line shows a realization of an event-based
# simulation, and the dashed line shows the behavior of the flow model
# (3.33). The maximum service rate is $\mu_{max} = 1$, and the arrival
# rate starts at $\lambda = 0.5$. The arrival rate is increased to $\lambda
# = 4$ at time 20, and it returns to $\lambda =0.5$ at time 25.
#

fig.add_subplot(gs[0, 1])       # first row, first column

# Construct the loading condition
t = np.linspace(0, 80, 100)

u =np.ones_like(t) * 0.5
u[t <= 25] = 4
u[t < 20] = 0.5

# Simulate the system dynamics
response = ct.input_output_response(queuing_sys, t, u)

# Plot the results
plt.plot(response.time, response.outputs, 'b-')

# Label the plot
plt.xlabel("Time $t$ [s]")
plt.ylabel(r"Queue length $x_{e}$")
plt.title("Overload condition")

# Save the figure
plt.savefig("figure-3.22-queuing_dynamics.png", bbox_inches='tight')