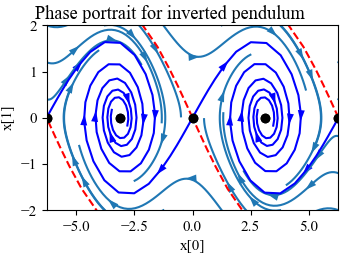
Figure 5.4: Equilibrium points for an inverted pendulum

Chapter	Dynamic Bevier
Figure number	5.4
Figure title	Equilibrium points for an inverted pendulum
GitHub URL	https://github.com/murrayrm/fbs2e-python/blob/main/figure-5.4-invpend phaseplot.py
Requires	python-control

Figure 5.4: Equilibrium points for an inverted pendulum. An inverted pendulum is a model for a class of balance systems in which we wish to keep a system upright, such as a rocket (a). Using a simplified model of an inverted pendulum (b), we can develop a phase portrait that shows the dynamics of the system (c). The system has multiple equilibrium points, marked by the solid dots along the x2 = 0 line.

# invepend_phaseplot.py - inverted pendulum phase plots
# RMM, 6 Apr 2024

import matplotlib.pyplot as plt
import numpy as np
from math import pi
import control as ct
import control.phaseplot as pp
import fbs                      # FBS plotting customizations

def invpend_update(t, x, u, params):
    m, l, b, g = params['m'], params['l'], params['b'], params['g']
    return [x[1], -b/m * x[1] + (g * l / m) * np.sin(x[0])]
invpend = ct.nlsys(
    invpend_update, states=2, inputs=0, name='inverted pendulum',
    params={'m': 1, 'l': 1, 'b': 0.2, 'g': 1})

fbs.figure()
ct.phase_plane_plot(
    invpend, [-2*pi, 2*pi, -2, 2], 4, gridspec=[6, 6],
    plot_separatrices={'timedata': 20, 'arrows': 4})
fbs.savefig('figure-5.4-invpend_phaseplotf.png')