Difference between revisions of "Figure 2.9: Responses to a unit step change in the reference signal for different values of the design parameters"
m |
m |
||
| Line 2: | Line 2: | ||
|Chapter=Feedback Principles | |Chapter=Feedback Principles | ||
|Figure number=2.9 | |Figure number=2.9 | ||
| − | |Figure title= | + | |Figure title=Responses to a unit step change in the reference signal for different values of the design parameters |
|GitHub URL=https://github.com/murrayrm/fbs2e-python/blob/main/figure-2.9-secord_stepresp.py | |GitHub URL=https://github.com/murrayrm/fbs2e-python/blob/main/figure-2.9-secord_stepresp.py | ||
}} | }} | ||
Revision as of 04:40, 3 July 2021
| Chapter | Feedback Principles |
|---|---|
| Figure number | 2.9 |
| Figure title | Responses to a unit step change in the reference signal for different values of the design parameters |
| GitHub URL | https://github.com/murrayrm/fbs2e-python/blob/main/figure-2.9-secord stepresp.py |
| Requires | python-control |
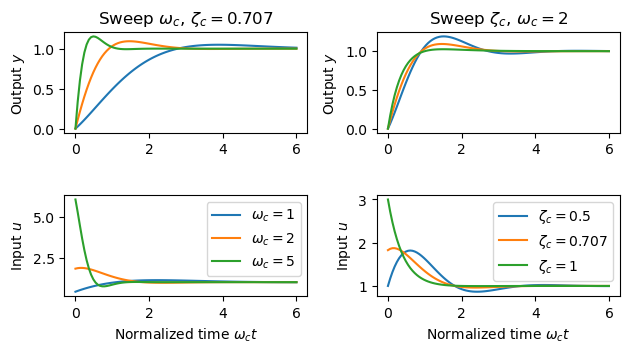
Figure 2.9: Responses to a unit step change in the reference signal for different values of the design parameters and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \zeta_\text{c}} . The left figure shows responses for fixed Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \zeta_\text{c} = } 0.707 and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \omega_\text{c} =} 1, 2, and 5. The right figure shows responses for Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \omega_\text{c} = } 2 and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \zeta_\text{c = }} 0.5, 0.707, and 1. The process parameters are Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a = b = 1} . The initial value of the control signal is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle k_\text{p}} .
# figure-2.9-secord_stepresp.py - step responses for second order systems
# RMM, 21 Jun 2021
#
# Responses to a unit step change in the reference signal for different
# values of the design parameters \omega_c and \zeta_c. The left column
# shows responses for fixed \zeta_c = 0.707 and \omega_c = 1, 2, and 5. The
# right figure column responses for \omega_c = 2 and \zeta_c = 0.5, 0.707,
# and 1. The process parameters are a = b = 1. The initial value of the
# control signal is kp.
#
import numpy as np
import matplotlib.pyplot as plt
import control as ct
# Process model
b = 1; a = 1
P = ct.tf([b], [1, a])
# Set the simulation time vector
time = np.linspace(0, 6, 100)
#
# Omega sweep
#
# Choose gains to use
wc_list = [1, 2, 5]
zc = 0.707
for wc in wc_list:
kp = (2 * zc * wc - a) / b
ki = wc**2
C = ct.tf([kp, ki], [1, 0])
Gyr = P*C / (1 + P*C)
Gur = C / (1 + P*C)
t, y = ct.step_response(Gyr, time)
t, u = ct.step_response(Gur, time)
if 'w_y_ax' not in locals():
w_y_ax = plt.subplot(3, 2, 1)
plt.ylabel('Output $y$')
plt.title("Sweep $\omega_c$, $\zeta_c = %g$" % zc)
w_y_ax.plot(t, y)
if 'w_u_ax' not in locals():
w_u_ax = plt.subplot(3, 2, 3)
plt.ylabel('Input $u$')
plt.xlabel('Normalized time $\omega_c t$')
w_u_ax.plot(t, u, label="$\omega_c = %g$" % wc)
# Label the omega sweep curves
w_u_ax.legend(loc="upper right")
#
# Zeta sweep
#
# Figure out frequency of critical damping
wc = 2
zc_list = [0.5, 0.707, 1]
# Plot results for different resonate frequencies
for zc in zc_list:
kp = (2 * zc * wc - a) / b
ki = wc**2
C = ct.tf([kp, ki], [1, 0])
Gyr = P*C / (1 + P*C)
Gur = C / (1 + P*C)
t, y = ct.step_response(Gyr, time)
t, u = ct.step_response(Gur, time)
if 'z_y_ax' not in locals():
z_y_ax = plt.subplot(3, 2, 2)
plt.ylabel('Output $y$')
plt.title("Sweep $\zeta_c$, $\omega_c = %g$" % wc)
z_y_ax.plot(t, y)
if 'z_u_ax' not in locals():
z_u_ax = plt.subplot(3, 2, 4)
plt.ylabel('Input $u$')
plt.xlabel('Normalized time $\omega_c t$')
z_u_ax.plot(t, u, label="$\zeta_c = %g$" % zc)
# Label the zeta sweep curves
z_u_ax.legend(loc="upper right")
# Overalll figure labeling
plt.tight_layout()