Difference between revisions of "Figure 5.7: Phase portrait and time domain simulation for a system with a single stable equilibrium point"
Jump to navigation
Jump to search
| (3 intermediate revisions by the same user not shown) | |||
| Line 7: | Line 7: | ||
}} | }} | ||
{| | {| | ||
| − | |- | + | |- align=top |
| rowspan=3 | [[Image:figure-5.7-stable_eqpt-pp.png]] | | rowspan=3 | [[Image:figure-5.7-stable_eqpt-pp.png]] | ||
| − | | <math> \begin{aligned} \dot x_1 &= x_2 \\ \dot x_2 &= -x_1 \end{aligned} </math> | + | | align=center | <math> \begin{aligned} \dot x_1 &= x_2 \\ \dot x_2 &= -2 x_1 \end{aligned} </math> |
| − | |- | + | |- align=bottom |
| rowspan=2 | [[Image:figure-5.7-stable_eqpt-time.png]] | | rowspan=2 | [[Image:figure-5.7-stable_eqpt-time.png]] | ||
|- | |- | ||
|} | |} | ||
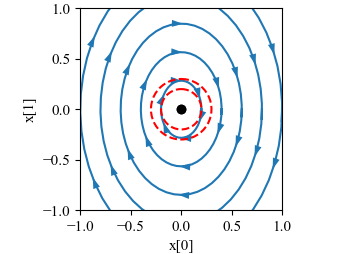
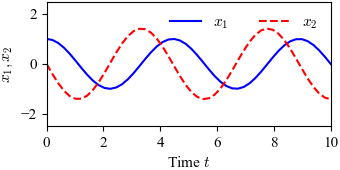
| + | '''Figure 5.7:''' Phase portrait and time domain simulation for a system with a single stable equilibrium point. The equilibrium point xe at the origin is stable since all trajectories that start near xe stay near xe. | ||
<nowiki> | <nowiki> | ||
| − | + | # stable_eqpt.py - plots for stable equlibrium point | |
| + | # RMM, 6 Apr 2024 | ||
| + | import matplotlib.pyplot as plt | ||
| + | import numpy as np | ||
| + | from math import pi | ||
| + | import control as ct | ||
| + | import control.phaseplot as pp | ||
| + | import fbs # FBS plotting customizations | ||
| − | + | m, b, k = 1, 0, 2 | |
| + | linsys = ct.ss([[0, 1], [-k/m, -b/m]], [[0], [1]], np.eye(2), 0) | ||
| − | + | # Draw the phase portrait | |
| + | fbs.figure() | ||
| + | ct.phase_plane_plot(linsys, [-1, 1, -1, 1], 1, plot_streamlines=False) | ||
| + | pp.streamlines( | ||
| + | linsys, np.array([[0.2, 0], [0.4, 0], [0.6, 0], [0.8, 0], [1, 0]]), | ||
| + | 4.5, arrows=6) | ||
| + | plt.gca().set_aspect('equal') | ||
| + | plt.suptitle("") | ||
| + | |||
| + | # Add some level sets | ||
| + | theta = np.linspace(0, 2*pi) | ||
| + | plt.plot(0.2 * np.sin(theta), 0.2 * np.cos(theta), 'r--') | ||
| + | plt.plot(0.3 * np.sin(theta), 0.3 * np.cos(theta), 'r--') | ||
| + | |||
| + | fbs.savefig('figure-5.7-stable_eqpt-pp.png') | ||
| + | |||
| + | fbs.figure('321') | ||
| + | plt.axis([0, 10, -2.5, 2.5]) | ||
| + | timepts = np.linspace(0, 10) | ||
| + | response = ct.input_output_response(linsys, timepts, 0, [1, 0]) | ||
| + | plt.plot(response.time, response.outputs[0], 'b', label="$x_1$") | ||
| + | plt.plot(response.time, response.outputs[1], 'r--', label="$x_2$") | ||
| + | plt.xlabel("Time $t$") | ||
| + | plt.ylabel("$x_1, x_2$") | ||
| + | plt.legend(loc='upper right', ncols=2, frameon=False) | ||
| + | fbs.savefig('figure-5.7-stable_eqpt-time.png') | ||
</nowiki> | </nowiki> | ||
Latest revision as of 16:02, 7 April 2024
| Chapter | Dynamic Behavior |
|---|---|
| Figure number | 5.7 |
| Figure title | 5.7: Phase portrait and time domain simulation for a system with a single stable equilibrium point |
| GitHub URL | https://github.com/murrayrm/fbs2e-python/blob/main/figure-5.7-stable-eqpt.py |
| Requires | python-control |
|
|
|
Figure 5.7: Phase portrait and time domain simulation for a system with a single stable equilibrium point. The equilibrium point xe at the origin is stable since all trajectories that start near xe stay near xe.
# stable_eqpt.py - plots for stable equlibrium point
# RMM, 6 Apr 2024
import matplotlib.pyplot as plt
import numpy as np
from math import pi
import control as ct
import control.phaseplot as pp
import fbs # FBS plotting customizations
m, b, k = 1, 0, 2
linsys = ct.ss([[0, 1], [-k/m, -b/m]], [[0], [1]], np.eye(2), 0)
# Draw the phase portrait
fbs.figure()
ct.phase_plane_plot(linsys, [-1, 1, -1, 1], 1, plot_streamlines=False)
pp.streamlines(
linsys, np.array([[0.2, 0], [0.4, 0], [0.6, 0], [0.8, 0], [1, 0]]),
4.5, arrows=6)
plt.gca().set_aspect('equal')
plt.suptitle("")
# Add some level sets
theta = np.linspace(0, 2*pi)
plt.plot(0.2 * np.sin(theta), 0.2 * np.cos(theta), 'r--')
plt.plot(0.3 * np.sin(theta), 0.3 * np.cos(theta), 'r--')
fbs.savefig('figure-5.7-stable_eqpt-pp.png')
fbs.figure('321')
plt.axis([0, 10, -2.5, 2.5])
timepts = np.linspace(0, 10)
response = ct.input_output_response(linsys, timepts, 0, [1, 0])
plt.plot(response.time, response.outputs[0], 'b', label="$x_1$")
plt.plot(response.time, response.outputs[1], 'r--', label="$x_2$")
plt.xlabel("Time $t$")
plt.ylabel("$x_1, x_2$")
plt.legend(loc='upper right', ncols=2, frameon=False)
fbs.savefig('figure-5.7-stable_eqpt-time.png')
