Difference between revisions of "Figure 2.9: Responses to a unit step change in the reference signal for different values of the design parameters"
Jump to navigation
Jump to search
m |
m |
||
| Line 2: | Line 2: | ||
|Chapter=Feedback Principles | |Chapter=Feedback Principles | ||
|Figure number=2.9 | |Figure number=2.9 | ||
| − | |Figure title= | + | |Figure title=Responses to a unit step change in the reference signal for different values of the design parameters |
|GitHub URL=https://github.com/murrayrm/fbs2e-python/blob/main/figure-2.9-secord_stepresp.py | |GitHub URL=https://github.com/murrayrm/fbs2e-python/blob/main/figure-2.9-secord_stepresp.py | ||
}} | }} | ||
Revision as of 04:40, 3 July 2021
| Chapter | Feedback Principles |
|---|---|
| Figure number | 2.9 |
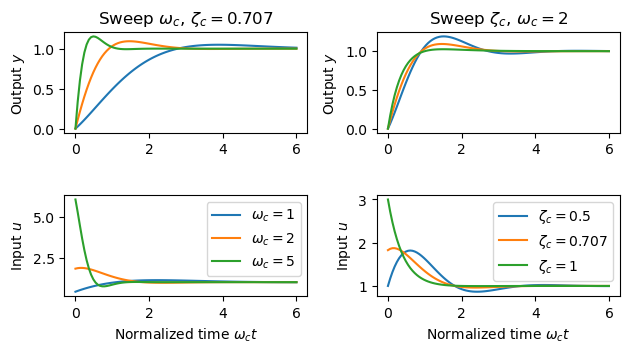
| Figure title | Responses to a unit step change in the reference signal for different values of the design parameters |
| GitHub URL | https://github.com/murrayrm/fbs2e-python/blob/main/figure-2.9-secord stepresp.py |
| Requires | python-control |
Figure 2.9: Responses to a unit step change in the reference signal for different values of the design parameters and . The left figure shows responses for fixed 0.707 and 1, 2, and 5. The right figure shows responses for 2 and 0.5, 0.707, and 1. The process parameters are . The initial value of the control signal is .
# figure-2.9-secord_stepresp.py - step responses for second order systems
# RMM, 21 Jun 2021
#
# Responses to a unit step change in the reference signal for different
# values of the design parameters \omega_c and \zeta_c. The left column
# shows responses for fixed \zeta_c = 0.707 and \omega_c = 1, 2, and 5. The
# right figure column responses for \omega_c = 2 and \zeta_c = 0.5, 0.707,
# and 1. The process parameters are a = b = 1. The initial value of the
# control signal is kp.
#
import numpy as np
import matplotlib.pyplot as plt
import control as ct
# Process model
b = 1; a = 1
P = ct.tf([b], [1, a])
# Set the simulation time vector
time = np.linspace(0, 6, 100)
#
# Omega sweep
#
# Choose gains to use
wc_list = [1, 2, 5]
zc = 0.707
for wc in wc_list:
kp = (2 * zc * wc - a) / b
ki = wc**2
C = ct.tf([kp, ki], [1, 0])
Gyr = P*C / (1 + P*C)
Gur = C / (1 + P*C)
t, y = ct.step_response(Gyr, time)
t, u = ct.step_response(Gur, time)
if 'w_y_ax' not in locals():
w_y_ax = plt.subplot(3, 2, 1)
plt.ylabel('Output $y$')
plt.title("Sweep $\omega_c$, $\zeta_c = %g$" % zc)
w_y_ax.plot(t, y)
if 'w_u_ax' not in locals():
w_u_ax = plt.subplot(3, 2, 3)
plt.ylabel('Input $u$')
plt.xlabel('Normalized time $\omega_c t$')
w_u_ax.plot(t, u, label="$\omega_c = %g$" % wc)
# Label the omega sweep curves
w_u_ax.legend(loc="upper right")
#
# Zeta sweep
#
# Figure out frequency of critical damping
wc = 2
zc_list = [0.5, 0.707, 1]
# Plot results for different resonate frequencies
for zc in zc_list:
kp = (2 * zc * wc - a) / b
ki = wc**2
C = ct.tf([kp, ki], [1, 0])
Gyr = P*C / (1 + P*C)
Gur = C / (1 + P*C)
t, y = ct.step_response(Gyr, time)
t, u = ct.step_response(Gur, time)
if 'z_y_ax' not in locals():
z_y_ax = plt.subplot(3, 2, 2)
plt.ylabel('Output $y$')
plt.title("Sweep $\zeta_c$, $\omega_c = %g$" % wc)
z_y_ax.plot(t, y)
if 'z_u_ax' not in locals():
z_u_ax = plt.subplot(3, 2, 4)
plt.ylabel('Input $u$')
plt.xlabel('Normalized time $\omega_c t$')
z_u_ax.plot(t, u, label="$\zeta_c = %g$" % zc)
# Label the zeta sweep curves
z_u_ax.legend(loc="upper right")
# Overalll figure labeling
plt.tight_layout()