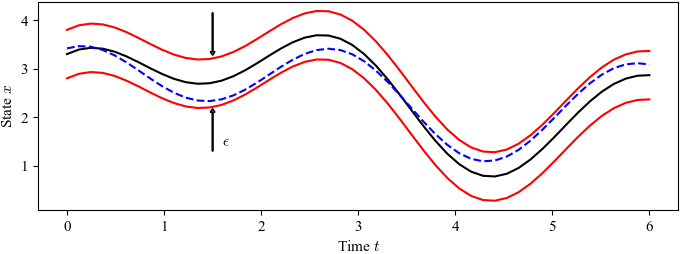
Figure 5.6: Illustration of Lyapunov’s concept of a stable solution

Chapter	Dynamic Behavior
Figure number	5.6
Figure title	Illustration of Lyapunov’s concept of a stable solution
GitHub URL	https://github.com/murrayrm/fbs2e-python/blob/main/figure-5-6-lyapunov stability.py
Requires	python-control

Figure 5.6: Illustration of Lyapunov’s concept of a stable solution. The solution represented by the solid line is stable if we can guarantee that all solutions remain within a tube of diameter ǫ by choosing initial conditions sufficiently close the solution.

# lyapunov_stability.py - illustration of Lyapunov stability
# RMM, 6 Apr 2024

import matplotlib.pyplot as plt
import numpy as np
import control as ct
import fbs                      # FBS plotting customizations

t = np.linspace(0, 6)
x0 = np.sin(t) + 0.8 * np.cos(2.2 * t) + 2.5

# Plot the centerline and bounds
fbs.figure('211')
plt.plot(t, x0, 'k')
plt.plot(t, x0 + 0.5, 'r', t, x0 - 0.5, 'r')

# Plot the signal
x = x0 - 0.4 * np.sin(t - 0.3)
plt.plot(t, x, 'b--')

# Label the axes
plt.xlabel("Time $t$")
plt.ylabel("State $x$")

# Add some arrows and label the range of stability
plt.arrow(1.5, 1.3, 0, 0.8, width=0.01, head_width=0.05)
plt.arrow(1.5, 4.15, 0, -0.8, width=0.01, head_width=0.05)
plt.text(1.6, 1.4, "$\\epsilon$")

fbs.savefig('figure-5.6-lyapunov_stability.png')