Errata: Example 8.10 missing factor of v, a1 and a2 flipped
Jump to navigation
Jump to search
| Chapter | Output Feedback |
|---|---|
| Page | 8-28 |
| Line | -4 |
| Version | 3.1.5 |
| Date | 6 Oct 2021 |
Example 8.10 (Steering control with velocity scheduling) is missing a factor of in the definition of that propagates through the example. In addition, the coefficients and are swapped in the definition of .
The equation for should read
This leads to an error in the definition of later in the example. In addition, the coefficients and are swapped and there was an error in the sign, so the definition of should be
The final controller then becomes
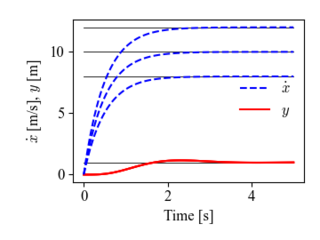
These corrections also change the controller response in Figure 8.13. The corrected response is
Acknowledgements: Thanks to Kaivalya Bakshi and Theunis Botha for pointing out the errors in this example.