Cruise control

This page documents the cruise control system that is used as a running example throughout the text. A detailed description of the dynamics of this system are presented in Chapter 4 - Examples. This page contains a description of the system, including the models and commands used to generate some of the plots in the text.

Introduction

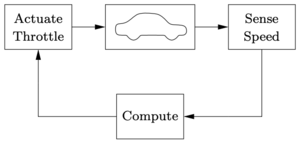
Cruise control is the term used to describe a control system that regulates the speed of an automobile. Cruise control was commercially introduced in 1958 as an option on the Chrysler Imperial. The basic operation of a cruise controller is to sense the speed of the vehicle, compare this speed to a desired reference, and then accelerate or decelerate the car as required. The figure to the right shows a block diagram of this feedback system.

File:Speedresp.png

The figure on the right shows how the velocity changes when the car travels on a horizontal road and the slope of the road changes to a constant uphill slope. The three different curves correspond to differing masses of the vehicle, between 1200 and 2000 kg, demonstrating that feedback can indeed compensate for the changing slope and that the closed loop system is robust to a large change in the vehicle characteristics.

Python code

 Code goes here 

A simple control algorithm for controlling the speed is to use a "proportional plus integral" feedback. In this algorithm, we choose the amount of gas flowing to the engine based on both the error between the current and desired speed, and the integral of that error. The plot on the right shows the results of this feedback for a step change in the desired speed and a variety of different masses for the car (which might result from having a different number of passengers or towing a trailer). Notice that independent of the mass (which varies by 25% of the total weight of the car), the steady state speed of the vehicle always approaches the desired speed and achieves that speed within approximately 10-15 seconds. Thus the performance of the system is robust with respect to this uncertainty.

Dynamic model

To develop a mathematical model we start with a force balance for the car body. Let $v$ be the speed of the car, $m$ the total mass (including passengers), $F$ the force generated by the contact of the wheels with the road, and $F_{\text{d}}$ the disturbance force due to gravity, friction and aerodynamic drag. The equation of motion of the car is simply

$m{\frac {dv}{dt}}=F-F_{\text{d}}.$

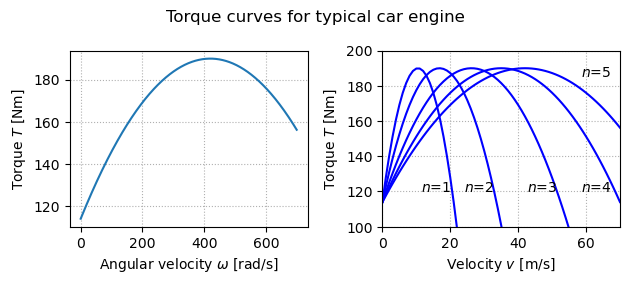
The force $F$ is generated by the engine, whose torque is proportional to the rate of fuel injection, which is itself proportional to a control signal $0\leq u\leq 1$ that controls the throttle position. The torque also depends on engine speed $\omega$. A simple representation of the torque at full throttle is given by the torque curve

$T(\omega )=T_{\text{m}}\left(1-\beta {\biggl (}{\frac {\omega }{\omega _{\text{m}}}}-1{\biggr )}^{2}\right),$

where the maximum torque $T_{\text{m}}$ is obtained at engine speed $\omega _{\text{m}}$. Typical parameters are $T_{m}=190$ Nm, $\omega _{m}$ = 420 rad/s (about 4000 RPM) and $\beta =0.4$.

Let $n$ be the gear ratio and $r$ the wheel radius. The engine speed is related to the velocity through the expression

$\omega ={\frac {n}{r}}v=:\alpha _{n}v,$

and the driving force can be written as

$F={\frac {nu}{r}}T(\omega )=\alpha _{n}uT(\alpha _{n}v).$

Typical values of $\alpha _{n}$ for gears 1 through 5 are $\alpha _{1}=40$, $\alpha _{2}=25$, $\alpha _{3}=16$, $\alpha _{4}=12$ and $\alpha _{5}=10$. The inverse of $\alpha _{n}$ has a physical interpretation as the effective wheel radius. The figure to the right shows the torque as a function of vehicle speed. The figure shows that the effect of the gear is to "flatten" the torque curve so that an almost full torque can be obtained almost over the whole speed range.

The disturbance force $F_{\text{d}}$ has three major components: $F_{\text{g}}$, the forces due to gravity; $F_{\text{r}}$, the forces due to rolling friction; and $F_{\text{a}}$, the aerodynamic drag. Letting the slope of the road be $\theta$, gravity gives the force $F_{\text{g}}=mg\sin \theta$, where $g=9.8\,{\text{m}}/{\text{s}}^{2}$ is the gravitational constant. A simple model of rolling friction is

$F_{\text{r}}=mgC_{\text{r}}\,{\text{sgn}}(v),$

where $C_{\text{r}}$ is the coefficient of rolling friction and sgn($v$) is the sign of $v$ or zero if $v=0$. A typical value for the coefficient of rolling friction is $C_{\text{r}}=0.01$. Finally, the aerodynamic drag is proportional to the square of the speed:

$F_{\text{a}}={\frac {1}{2}}\rho C_{\text{d}}Av^{2},$

where $\rho$ is the density of air, $C_{d}$ is the shape-dependent aerodynamic drag coefficient and $A$ is the frontal area of the car. Typical parameters are $\rho =$ 1.3 k/m${}^{3}$, $C_{\text{d}}=0.32$ and $A=$ 2.4 m${}^{2}$.

Python code

The model for the system above can be built using the Python Control Toolbox. The code blocks in this section can be used to generate the plots above.

Package initialization

 import numpy as np
 import matplotlib.pyplot as plt
 from math import pi
 import control as ct

Vehicle model

 def vehicle_update(t, x, u, params={}):
     """Vehicle dynamics for cruise control system.
 
     Parameters
     ----------
     x : array
          System state: car velocity in m/s
     u : array
          System input: [throttle, gear, road_slope], where throttle is
          a float between 0 and 1, gear is an integer between 1 and 5,
          and road_slope is in rad.
 
     Returns
     -------
     float
         Vehicle acceleration
     """
 
     from math import copysign, sin
     sign = lambda x: copysign(1, x)         # define the sign() function
     
     # Set up the system parameters
     m = params.get('m', 1600.)              # vehicle mass, kg
     g = params.get('g', 9.8)                # gravitational constant, m/s^2
     Cr = params.get('Cr', 0.01)             # coefficient of rolling friction
     Cd = params.get('Cd', 0.32)             # drag coefficient
     rho = params.get('rho', 1.3)            # density of air, kg/m^3
     A = params.get('A', 2.4)                # car area, m^2
     alpha = params.get(
         'alpha', [40, 25, 16, 12, 10])      # gear ratio / wheel radius
 
     # Define variables for vehicle state and inputs
     v = x[0]                           # vehicle velocity
     throttle = np.clip(u[0], 0, 1)     # vehicle throttle
     gear = u[1]                        # vehicle gear
     theta = u[2]                       # road slope
 
     # Force generated by the engine
     omega = alpha[int(gear)-1] * v      # engine angular speed
     F = alpha[int(gear)-1] * motor_torque(omega, params) * throttle
 
     # Disturbance forces
     #
     # The disturbance force Fd has three major components: Fg, the forces due
     # to gravity; Fr, the forces due to rolling friction; and Fa, the
     # aerodynamic drag.
 
     # Letting the slope of the road be \theta (theta), gravity gives the
     # force Fg = m g sin \theta.
     Fg = m * g * sin(theta)
 
     # A simple model of rolling friction is Fr = m g Cr sgn(v), where Cr is
     # the coefficient of rolling friction and sgn(v) is the sign of v (±1) or
     # zero if v = 0.
     Fr  = m * g * Cr * sign(v)
 
     # The aerodynamic drag is proportional to the square of the speed: Fa =
     # 1/2 \rho Cd A |v| v, where \rho is the density of air, Cd is the
     # shape-dependent aerodynamic drag coefficient, and A is the frontal area
     # of the car.
     Fa = 1/2 * rho * Cd * A * abs(v) * v
     
     # Final acceleration on the car
     Fd = Fg + Fr + Fa
     dv = (F - Fd) / m
     
     return dv

Engine model

 def motor_torque(omega, params={}):
     # Set up the system parameters
     Tm = params.get('Tm', 190.)             # engine torque constant
     omega_m = params.get('omega_m', 420.)   # peak engine angular speed
     beta = params.get('beta', 0.4)          # peak engine rolloff
 
     return np.clip(Tm * (1 - beta * (omega/omega_m - 1)**2), 0, None)

Input/output model for the vehicle system

 vehicle = ct.NonlinearIOSystem(
     vehicle_update, None, name='vehicle',
     inputs = ('u', 'gear', 'theta'), outputs = ('v'), states=('v'))

Input/output torque curves (plot)

 # Figure 4.2a - single torque curve as function of omega
 omega_range = np.linspace(0, 700, 701)
 plt.subplot(2, 2, 1)
 plt.plot(omega_range, [motor_torque(w) for w in omega_range])
 plt.xlabel('Angular velocity $\omega$ [rad/s]')
 plt.ylabel('Torque $T$ [Nm]')
 plt.grid(True, linestyle='dotted')
 
 # Figure 4.2b - torque curves in different gears, as function of velocity
 plt.subplot(2, 2, 2)
 v_range = np.linspace(0, 70, 71)
 alpha = [40, 25, 16, 12, 10]
 for gear in range(5):
     omega_range = alpha[gear] * v_range
     plt.plot(v_range, [motor_torque(w) for w in omega_range],
              color='blue', linestyle='solid')
 
 # Set up the axes and style
 plt.axis([0, 70, 100, 200])
 plt.grid(True, linestyle='dotted')
 
 # Add labels
 plt.text(11.5, 120, '$n$=1')
 plt.text(24, 120, '$n$=2')
 plt.text(42.5, 120, '$n$=3')
 plt.text(58.5, 120, '$n$=4')
 plt.text(58.5, 185, '$n$=5')
 plt.xlabel('Velocity $v$ [m/s]')
 plt.ylabel('Torque $T$ [Nm]')
 
 plt.suptitle('Torque curves for typical car engine');
 plt.tight_layout()

PI controller

 # Construct a PI controller with rolloff, as a transfer function
 Kp = 0.5                        # proportional gain
 Ki = 0.1                        # integral gain
 control_tf = ct.tf2io(
     ct.TransferFunction([Kp, Ki], [1, 0.01*Ki/Kp]),
     name='control', inputs='u', outputs='y')
 
 cruise_tf = ct.InterconnectedSystem(
     (vehicle, control_tf), name='cruise',
     connections = [('control.u', '-vehicle.v'), ('vehicle.u', 'control.y')],
     inplist = ('control.u', 'vehicle.gear', 'vehicle.theta'), inputs = ('vref', 'gear', 'theta'),
     outlist = ('vehicle.v', 'vehicle.u'), outputs = ('v', 'u'))

Plotting function

 # Define a generator for creating a "standard" cruise control plot
 def cruise_plot(sys, t, y, t_hill=5, vref=20, antiwindup=False, linetype='b-',
                subplots=[None, None]):
     # Figure out the plot bounds and indices
     v_min = vref-1.2; v_max = vref+0.5; v_ind = sys.find_output('v')
     u_min = 0; u_max = 2 if antiwindup else 1; u_ind = sys.find_output('u')
 
     # Make sure the upper and lower bounds on v are OK
     while max(y[v_ind]) > v_max: v_max += 1
     while min(y[v_ind]) < v_min: v_min -= 1
         
     # Create arrays for return values
     subplot_axes = subplots.copy()
 
     # Velocity profile
     if subplot_axes[0] is None:
         subplot_axes[0] = plt.subplot(2, 1, 1)
     else:
         plt.sca(subplots[0])
     plt.plot(t, y[v_ind], linetype)
     plt.plot(t, vref*np.ones(t.shape), 'k-')
     plt.plot([t_hill, t_hill], [v_min, v_max], 'k--')
     plt.axis([0, t[-1], v_min, v_max])
     plt.xlabel('Time $t$ [s]')
     plt.ylabel('Velocity $v$ [m/s]')
 
     # Commanded input profile
     if subplot_axes[1] is None:
         subplot_axes[1] = plt.subplot(2, 1, 2)
     else:
         plt.sca(subplots[1])
     plt.plot(t, y[u_ind], 'r--' if antiwindup else linetype)
     plt.plot([t_hill, t_hill], [u_min, u_max], 'k--')
     plt.axis([0, t[-1], u_min, u_max])
     plt.xlabel('Time $t$ [s]')
     plt.ylabel('Throttle $u$')
 
     # Applied input profile
     if antiwindup:
         plt.plot(t, np.clip(y[u_ind], 0, 1), linetype)
         plt.legend(['Commanded', 'Applied'], frameon=False)
         
     return subplot_axes

Simulated responses

 # Define the time and input vectors
 T = np.linspace(0, 25, 101)
 vref = 20 * np.ones(T.shape)
 gear = 4 * np.ones(T.shape)
 theta0 = np.zeros(T.shape)
 
 # Now simulate the effect of a hill at t = 5 seconds
 plt.figure()
 plt.suptitle('Response to change in road slope')
 theta_hill = np.array([
     0 if t <= 5 else
     4./180. * pi * (t-5) if t <= 6 else
     4./180. * pi for t in T])
 
 subplots = [None, None]
 linecolor = ['red', 'blue', 'green']
 handles = []
 for i, m in enumerate([1200, 1600, 2000]):
     # Compute the equilibrium state for the system
     X0, U0 = ct.find_eqpt(
         cruise_tf, [vref[0], 0], [vref[0], gear[0], theta0[0]], 
         iu=[1, 2], y0=[vref[0], 0], iy=[0], params={'m':m})
 
     t, y = ct.input_output_response(
         cruise_tf, T, [vref, gear, theta_hill], X0, params={'m':m})
 
     subplots = cruise_plot(cruise_tf, t, y, t_hill=5, subplots=subplots,
                            linetype=linecolor[i][0] + '-')
     handles.append(mlines.Line2D([], [], color=linecolor[i], linestyle='-', 
                                  label="m = %d" % m))
 
 # Add labels to the plots
 plt.sca(subplots[0])
 plt.ylabel('Speed [m/s]')
 plt.legend(handles=handles, frameon=False, loc='lower right');
 
 plt.sca(subplots[1])
 plt.ylabel('Throttle')
 plt.xlabel('Time [s]');

Linearized Dynamics

To explore the behavior of the cruise control system near the equilibrium point we will linearize the system. A Taylor series expansion of the dynamics around the equilibrium point gives

${\frac {d(v-v_{\text{e}})}{dt}}=-a(v-v_{\text{e}})-b_{\text{g}}(\theta -\theta _{\text{e}})+b(u-u_{\text{e}})+{\text{higher-order terms,}}$

where

$a={\frac {\rho C_{\text{d}}A|v_{\text{e}}|-u_{\text{e}}\alpha _{n}^{2}T'(\alpha _{n}v_{\text{e}})}{m}},\qquad b_{\text{g}}=g\cos {\theta _{\text{e}}},\qquad b={\frac {\alpha _{n}T(\alpha _{n}v_{\text{e}})}{m}}.$

Notice that the term corresponding to rolling friction disappears if $v>0$. For a car in fourth gear with $v_{\text{e}}=20$ m/s,$\theta _{\text{e}}=0$, and the numerical values for the car from \exampsecref{cruise}, the equilibrium value for the throttle is $u_{\text{e}}=0.1687$ and the parameters are $a=0.01$, $b=1.32$, and $b_{\text{g}}=9.8$$. This linear model describes how small perturbations in the velocity about the nominal speed evolve in time.

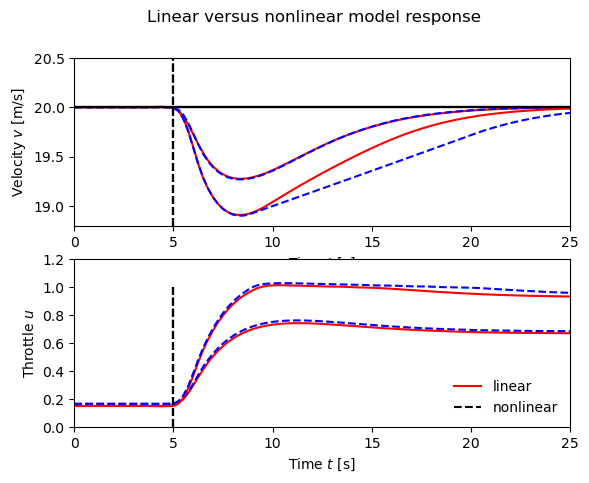
We apply the PI controller above to the case where the car is running with constant speed on a horizontal road and the system has stabilized so that the vehicle speed and the controller output are constant. The figure to the right shows what happens when the car encounters a hill with a slope of 4 degrees and a hill with a slope of 6 degrees at time $t=\,$ 5 seconds. The results for the nonlinear model are solid curves and those for the linear model are dashed curves. The differences between the curves are very small (especially for $\theta =\,$ 4 degrees), and control design based on the linearized model is thus validated.

Python code

Linearized dynamics

 # Find the equilibrium point for the system
 Xeq, Ueq = ct.find_eqpt(
     vehicle, [vref[0]], [0, gear[0], theta0[0]], y0=[vref[0]], iu=[1, 2])
 print("Xeq = ", Xeq)
 print("Ueq = ", Ueq)
 
 # Compute the linearized system at the eq pt
 vehicle_linearized = ct.linearize(vehicle, Xeq, [Ueq[0], gear[0], 0])

 # Create a closed loop controller for the linear system
 cruise_linearized = ct.InterconnectedSystem(
     (vehicle_linearized, control_tf), name='cruise_linearized',
     connections = [('control.u', '-vehicle.v'), ('vehicle.u', 'control.y')],
     inplist = ('control.u', 'vehicle.gear', 'vehicle.theta'), 
         inputs = ('vref', 'gear', 'theta'),
     outlist = ('vehicle.v', 'vehicle.u'), outputs = ('v', 'u'))

Simulations

 # Nonlinear response
 cruise_plot(cruise_tf, t, y, t_hill=5, subplots=subplots,
                           linetype=linecolor[i][0] + '-')

Further Reading

• How Stuff Works: cruise control
• Wikipedia: cruise control