Difference between revisions of "Cruise control"
| Line 46: | Line 46: | ||
where <math>\rho</math> is the density of air, <math>C_d</math> is the shape-dependent aerodynamic drag coefficient and <math>A</math> is the frontal area of the car. Typical parameters are <math>\rho = </math> 1.3 k/m<math>{}^3</math>, <math>C_\text{d} = 0.32</math> and <math>A =</math> 2.4 m<math>{}^2</math>. | where <math>\rho</math> is the density of air, <math>C_d</math> is the shape-dependent aerodynamic drag coefficient and <math>A</math> is the frontal area of the car. Typical parameters are <math>\rho = </math> 1.3 k/m<math>{}^3</math>, <math>C_\text{d} = 0.32</math> and <math>A =</math> 2.4 m<math>{}^2</math>. | ||
| − | === Python | + | === Python code === |
The model for the system above can be built using the [[https:python-control.org|Python Control Toolbox]]. The code blocks in this section can be used to generate the plots above. | The model for the system above can be built using the [[https:python-control.org|Python Control Toolbox]]. The code blocks in this section can be used to generate the plots above. | ||
| Line 235: | Line 235: | ||
}} | }} | ||
| − | == | + | == Linearized Dynamics == |
| − | + | ||
| − | + | To explore the behavior of the cruise control system near the equilibrium point we | |
| + | will linearize the system. A Taylor series expansion of | ||
| + | the dynamics around the equilibrium point gives | ||
| + | <center><math> | ||
| + | \frac{d(v-v_\text{e})}{dt} = -a (v - v_\text{e}) | ||
| + | - b_\text{g} (\theta - \theta_\text{e}) + b (u - u_\text{e}) | ||
| + | + \text{higher-order terms,} | ||
| + | </math></center> | ||
| + | where | ||
| + | <center><math> | ||
| + | a = \frac{\rho C_\text{d} A |v_\text{e}| | ||
| + | - u_\text{e} \alpha_n^2 T'(\alpha_n v_\text{e})}{m}, \qquad | ||
| + | b_\text{g} = g \cos{\theta_\text{e}}, \qquad | ||
| + | b = \frac{\alpha_n T(\alpha_n v_\text{e})}{m}. | ||
| + | </math></center> | ||
| + | Notice that the term corresponding to rolling friction disappears if <math>v > 0</math>. For a car in fourth gear with <math>v_\text{e} = 20</math> m/s,<math>\theta_\text{e} = 0</math>, and the numerical values for the car from \exampsecref{cruise}, the equilibrium value for the throttle is <math>u_\text{e}=0.1687</math> and the parameters are <math>a = 0.01</math>, <math>b = 1.32</math>, and <math>b_\text{g} = 9.8</math>$. This linear model describes how small perturbations in the velocity about the nominal speed evolve in time. | ||
| + | |||
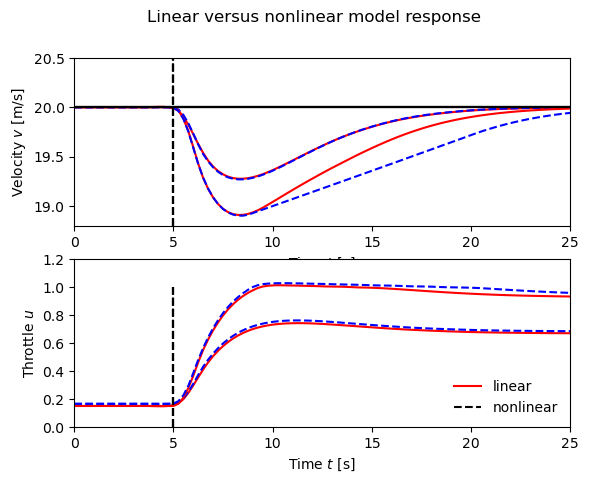
| + | [[Image:cruise-linear_vs_nonlinear.png|right|Simulated response of a vehicle with PI cruise control as it climbs a hill with a slope of 4 degrees (smaller velocity deviation/throttle) and a slope of 6 degrees (larger velocity deviation/throttle). The solid line is the simulation based on a nonlinear model, and the dashed line shows the corresponding simulation using a linear model. The controller gains are <math>k_\text{p}=0.5</math> and <math>k_\text{i}=0.1</math> and include anti-windup compensation (described in more detail in below).]] | ||
| + | We apply the PI controller above to the case where the car is running with constant speed on a horizontal road and the system has stabilized so that the vehicle speed and the controller output are constant. The figure to the right shows what happens when the car encounters a hill with a slope of 4 degrees and a hill with a slope of 6 degrees at time <math>t =\,</math> 5 seconds. The results for the nonlinear model are solid curves and those for the linear model are dashed curves. The differences between the curves are very small (especially for <math>\theta =\,</math> 4 degrees), and control design based on the linearized model is thus validated. | ||
| + | |||
| + | === Python code === | ||
| + | |||
| + | {{Code block|Linearized dynamics| | ||
| + | # Define the time and input vectors | ||
| + | T = np.linspace(0, 25, 501) | ||
| + | vref = 20 * np.ones(T.shape) | ||
| + | gear = 4 * np.ones(T.shape) | ||
| + | theta0 = np.zeros(T.shape) | ||
| + | |||
| + | # Find the equilibrium point for the system | ||
| + | Xeq, Ueq = ct.find_eqpt( | ||
| + | vehicle, [vref[0]], [0, gear[0], theta0[0]], y0=[vref[0]], iu=[1, 2]) | ||
| + | print("Xeq = ", Xeq) | ||
| + | print("Ueq = ", Ueq) | ||
| + | |||
| + | # Compute the linearized system at the eq pt | ||
| + | cruise_linearized = ct.linearize(vehicle, Xeq, [Ueq[0], gear[0], 0]) | ||
| + | }} | ||
| + | |||
| + | {{Code block|Simulations| | ||
| + | }} | ||
| + | |||
| + | == State Space Control == | ||
== Further Reading == | == Further Reading == | ||
Revision as of 06:56, 29 December 2020
This page documents the cruise control system that is used as a running example throughout the text. A detailed description of the dynamics of this system are presented in Chapter 4 - Examples. This page contains a description of the system, including the models and commands used to generate some of the plots in the text.
Introduction
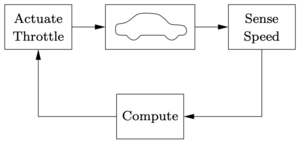
Cruise control is the term used to describe a control system that regulates the speed of an automobile. Cruise control was commercially introduced in 1958 as an option on the Chrysler Imperial. The basic operation of a cruise controller is to sense the speed of the vehicle, compare this speed to a desired reference, and then accelerate or decelerate the car as required. The figure to the right shows a block diagram of this feedback system.
A simple control algorithm for controlling the speed is to use a "proportional plus integral" feedback. In this algorithm, we choose the amount of gas flowing to the engine based on both the error between the current and desired speed, and the integral of that error. The plot on the right shows the results of this feedback for a step change in the desired speed and a variety of different masses for the car (which might result from having a different number of passengers or towing a trailer). Notice that independent of the mass (which varies by 25% of the total weight of the car), the steady state speed of the vehicle always approaches the desired speed and achieves that speed within approximately 10-15 seconds. Thus the performance of the system is robust with respect to this uncertainty.
Dynamic model
To develop a mathematical model we start with a force balance for the car body. Let be the speed of the car, the total mass (including passengers), the force generated by the contact of the wheels with the road, and the disturbance force due to gravity, friction and aerodynamic drag. The equation of motion of the car is simply
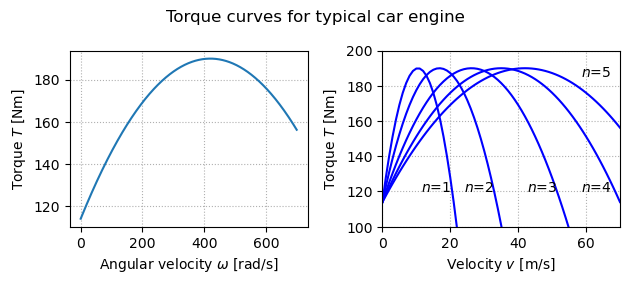
The force is generated by the engine, whose torque is proportional to the rate of fuel injection, which is itself proportional to a control signal that controls the throttle position. The torque also depends on engine speed . A simple representation of the torque at full throttle is given by the torque curve
where the maximum torque is obtained at engine speed . Typical parameters are Nm, = 420 rad/s (about 4000 RPM) and .
Let be the gear ratio and the wheel radius. The engine speed is related to the velocity through the expression
and the driving force can be written as
Typical values of for gears 1 through 5 are , , , and . The inverse of has a physical interpretation as the effective wheel radius. The figure to the right shows the torque as a function of vehicle speed. The figure shows that the effect of the gear is to "flatten" the torque curve so that an almost full torque can be obtained almost over the whole speed range.
The disturbance force has three major components: , the forces due to gravity; , the forces due to rolling friction; and , the aerodynamic drag. Letting the slope of the road be , gravity gives the force , where is the gravitational constant. A simple model of rolling friction is
where is the coefficient of rolling friction and sgn() is the sign of or zero if . A typical value for the coefficient of rolling friction is . Finally, the aerodynamic drag is proportional to the square of the speed:
where is the density of air, is the shape-dependent aerodynamic drag coefficient and is the frontal area of the car. Typical parameters are 1.3 k/m, and 2.4 m.
Python code
The model for the system above can be built using the Python Control Toolbox. The code blocks in this section can be used to generate the plots above.
Linearized Dynamics
To explore the behavior of the cruise control system near the equilibrium point we will linearize the system. A Taylor series expansion of the dynamics around the equilibrium point gives
where
Notice that the term corresponding to rolling friction disappears if . For a car in fourth gear with m/s,, and the numerical values for the car from \exampsecref{cruise}, the equilibrium value for the throttle is and the parameters are , , and $. This linear model describes how small perturbations in the velocity about the nominal speed evolve in time.
We apply the PI controller above to the case where the car is running with constant speed on a horizontal road and the system has stabilized so that the vehicle speed and the controller output are constant. The figure to the right shows what happens when the car encounters a hill with a slope of 4 degrees and a hill with a slope of 6 degrees at time 5 seconds. The results for the nonlinear model are solid curves and those for the linear model are dashed curves. The differences between the curves are very small (especially for 4 degrees), and control design based on the linearized model is thus validated.
Python code
State Space Control
Further Reading
- How Stuff Works: cruise control
- Wikipedia: cruise control